Matematika

BELAJAR MATEMATIKA

Apa itu matematika ???

• Pengertian matematika menurut kamus besar Bahasa Indonesia adalah ilmu tentang bilangan-bilangan, hubungan antar bilangan dan prosedur operasionalyang digunakan dalam penyelesaian masalah bilangan. Dalam perkembangannya bilangan ini diaplikasikan ke bidang ilmu-ilmu lain sesuai penggunaannya. 
• Menurut James dan James (1976), matematika diartikan sebagai ilmu logika mengenai bentuk, susunan, besaran, dan konsep-konsep yang saling berubungan satu sama lainnya dengan jumlah yang terbagi ke dalam tiga bidang yaitu aljabar, analisis, dan geometri.
• Sedangkan menurut Reys dkk. (1984), matematika diartikan sebagai analisis suatu pola dan hubungannya, suatu jalan atau pola berpikir, suatu seni, suatu bahasa, dan suatu alat. 
• Berdasarkan pengertian-pengertian tentang matematika tersebut maka matematika dapat diartikan sebagai suatu ilmu yang mempelajari bilangan dan bangun serta konsep-konsep yang berkenaan dengan kebenarannya secara logika menggunakan simbol-simbol yang umum serta aplikasi dalam bidang lainnya. 
•  Pendidikan matematika dapat diartikan sebagai proses perubahan baik kognitif, afektif, dan kognitif kearah kedewasaan sesuai dengan kebenaran logika. 

Peran serta pendidikan matematika dalam pendidikan secara keseluruhan sangat luas tidak hanya berkaitan tentang hal yang teknis dan ilmiah saja. Buktinya bahwa persoalan-persoalan dalam kehidupan sehari-hari dapat diuraikan dalam model matematika sehingga penyelesaiannya lebih cepat dan sederhana. Hal ini sesuai dengan tujuan pengajaran matematika di sekolah yang tertuang dalam kurikulum bahwa matematika melatih siswa untuk berpikir kritis, kreatif, inovatif, dan mampu menyelesaikan masalah dengan tepat dan singkat serta dapat dipertanggungjawabkan. 

Menurut H. Winter (1972), siswa seharusnya belajar berargumentasi, mengerti apa yang dibicarakan, memahami lalu dapat mengabstraksikannya sehingga menyeimbangkan penggunaan otak kiri dan otak kanan (otak kiri digunakan untuk menghitung dan otak kanan untuk kreatifitas) untuk mematematisasikan situasi di sekelilingnya. Sehingga guru harus mampu berkomunikasi dengan baik dalam kegiatan pembelajaran agar materi atau konsep yang disampaikan tidak disalahterimakan siswa. Hal ini agar pengajaran matematika tidak membosankan, menarik, dan menyenangkan. 

Ada beberapa karakteristik matematika, antara lain : 

1. Objek yang dipelajari abstrak. 

Sebagian besar yang dipelajari dalam matematika adalah angka atau bilangan yang secara nyata tidak ada atau merupakan hasil pemikiran otak manusia. Menurut Cockroft (1982), matematika sulit dipelajari dan sulit diajarkan karena objek yang dipelajari bersifat abstrak yaitu angka atau bilangan dan memiliki hirarki yang tegas serta banyak manipulasi lambang, sehingga Guru harus dapat mengembangkan kualitas pribadi dan siswanya secara keseluruhan, yaitu : Kebiasaan bekerja dengan baik seperti : imajinatif, kreatif, dan fleksibel, sistematik, independen dalam berpikir dan bertindak, bekerja sama, dan cermat. Serta sikap positif terhadap matematika antara lain : terpesona dengan matematika; berminat dan termotivasi; gembira dan menyukai matematik; menghargai maksud, kekuatan, dan relevansi matematika dalam kehidupan; kepuasan yang tumbuh dari keberhasilan dan keyakinan akan kemampuannya mengerjakan matematika. 

2. Kebenaranya berdasarkan logika. 

Kebenaran dalam matematika adalah kebenaran secara logika bukan empiris. Artinya kebenarannya tidak dapat dibuktikan melalui ekserimen seperti dalam ilmu fisika atau biologi. Contohnya nilai √-2 tidak dapat dibuktikan dengan kalkulator, tetapi secara logika ada jawabannya sehingga bilangan tersebut dinamakan bilangan imajiner (khayal). 

3. Pembelajarannya secara bertingkat dan kontinu. 

Pemberian atau penyajian materi matematika disesuaikan dengan tingkatan pendidikan dan dilakukan secara terus-menerus. Artinya dalam mempelajari matematika harus secara berulang melalui latihan-latihan soal. 

4. Ada keterkaitan antara materi yang satu dengan yang lainnya. 

Materi yang akan dipelajari harus memenuhi atau menguasai materi sebelumnya. Contohnya ketika akan mempelajari tentang volume atau isi suatu bangun ruang maka harus menguasai tentang materi luas dan keliling bidang datar. 

5. Menggunakan bahasa simbol. 

Dalam matematika penyampaian materi menggunakan simbol-simbol yang telah disepakati dan dipahami secara umum. Misalnya penjumlahan menggunakan simbol "+" sehingga tidak terjadi dualisme jawaban. 

6. Diaplikasikan dibidang ilmu lain. 

Matematika dapat digunakan untuk menyeleksi atau menyaring data yang ada. Seperti tes seleksi calon PNS, Polisi, TNI, pelajar, mahasaiswa atau karyawan menggunakan tes tulis dengan materi matematika (biasanya logika dan berhitung) untuk mengetahui kemampuan berpikir cepat dan dapat menyelesaikan masalah. Dalam bidang teknik matematika digunakan seperti teknik informatika atau komputer menggunakan konsep bilangan basis, teknik industri atau mesin matematika digunakan untuk menentukan ketelitian suatu alat ukur atau perkakas yang digunakan. 

Menurut Andrea J. O'Connor bahwa "Mathematic is used by engineers to solve a very wide range of problem, including design calculations for building, machines, electronic components or chemical plants". Bidang ekonomi menggunakan konsep fungsi untuk memprediksikan produksi maupun penjualan.

BEBERAPA MACAM MATEMATIKA:

A. Aritmatika

Aritmatika merupakan materi pertama yang dikembangkan dan menjadi ilmu dasar dari semua pelajaran matematika modern. Sejak 2000 SM, banyak peradaban, seperti Babylonia, China, Yunani, Mesir, hingga Arab, sudah mengembangkan aritmatika untuk mendukung kehidupan mereka.
Sejak saat itu, aritmatika terus berkembang. Di era modern, aritmatika akan kamu dapatkan di jenjang Sekolah Dasar (SD) hingga Sekolah Menengah Pertama (SMP). Di jenjang tersebut, kamu akan mempelajari mengenai teori aritmatika dan rumus matematika lengkap dengan soal-soalnya.
Di sini, kamu bisa belajar aritmatika dengan cara cara yang mudah melalui video pembelajaran yang interatif dan menarik. Materi yang akan diajarkan antara lain: teori bilangan, FPB & KPK, aritmatika sosial, dan barisan & deret.

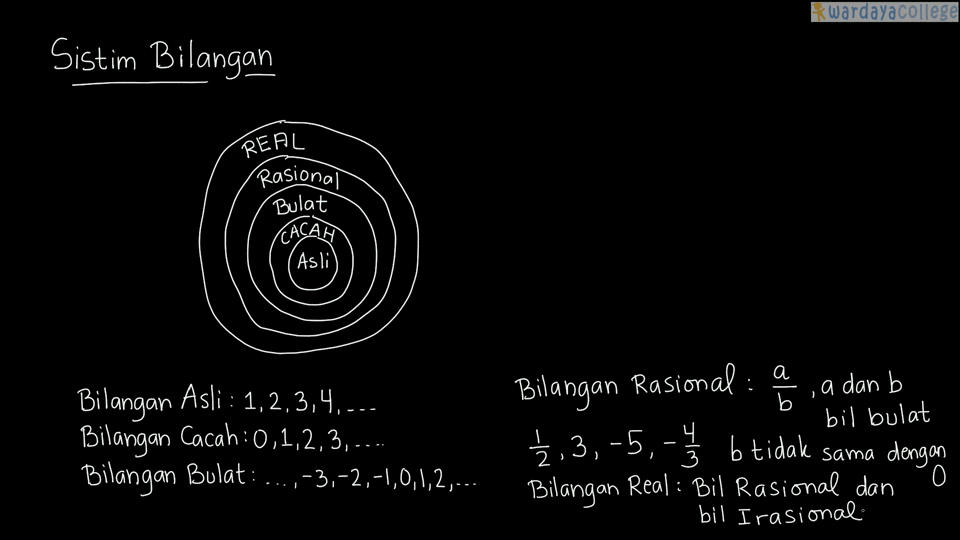
1. Bilangan

Materi ini akan berfokus pada angka. Pelajaran akan dimulai dengan pengenalan jenis-jenis bilangan, seperti: bilangan bulat, bilangan cacah, bilangan riil, bilangan asli, bilangan prima, dan bilangan pecahan.
Materi bilangan berlanjut dengan menerangkan mengenai operasi pengolahan angka, seperti penjumlahan, pengurangan, perkalian, dan pembagian. Di materi ini, kamu akan mendapatkan rumus aritmatika dasar yang harus kamu kuasai sebelum mempelajari materi matematika lainnya.
Kamu bisa mendapatkan semua materi bilangan di sini, lengkap dengan rumus aritmatika dasar. Teknik penghitungan bilangan yang disampaikan mudah dimengerti dan mudah dipraktekan.

2. FPB & KPK

Materi berikutnya adalah faktor persekutuan terbesar (FPB) dan kelipatan persekutuan terkecil (KPK). FPB dimaksudkan untuk mencari bilangan yang mampu membagi 2 bilangan atau lebih sama rata, sedangkan KPK dimaksudkan untuk mencari kelipatan yang sama dari 2 bilangan atau lebih.
Materi FPB dan KPK ini sangat berguna untuk kamu di materi lainnya, terutama pecahan. Dengan menguasai FPB, kamu akan dengan mudah menyederhanakan pecahan ke bentuk yang paling sederhana.
Ada 2 teknik yang bisa kamu gunakan dalam mencari FPB dan KPK, yaitu dengan mengurutkan bilangan ataupun dengan pohon faktor. Kedua rumus aritmatika dasar ini bisa kamu pelajari di sini.

3. Pecahan

Pecahan merupakan bilangan yang memiliki ciri khusus yang membedakan dari bilangan lain, yaitu bilangan pecahan memiliki pembilang dan penyebut. Bilangan pecahan digunakan untuk menyebutkan sesuatu yang tidak utuh, misalnya separuh bisa dikatakan dengan ½.
Ada 4 cara untuk melakukan operasi pengolahan bilangan pecahan, yaitu penjumlahan, pengurangan, perkalian, dan pembagian. Di materi ini, kamu juga dituntut untuk terampil dalam menyederhanakan pecahan dan merubah pecahan ke dalam bentuk desimal atau persen.

4. Bilangan Desimal & Persentase

Bilangan desimal & presentase merupakan jenis bilangan yang memiliki ciri khas masing-masing. Bilangan desimal identik dengan penggunaan koma (,) diantara bilangannya dan bilangan persen memiliki tanda persen/ per seratus (%).
Bilangan desimal dan bilangan persen juga berhubungan dengan bilangan pecahan. Kamu akan belajar bagaimana cara merubah bilangan desimal menjadi pecahan, merubah bilangan persen ke bilangan pecahan, merubah bilangan desimal ke bilangan persentase.
Tak perlu khawatir, kamu akan mendapatkan materi ini di video pembelajaran wardayacollege.com, beserta dengan rumusnya. Setelah mahir dengan rumusnya, kamu bisa langsung mengerjakan soal soal aritmatika mengenai desimal dan persentase. Enjoy!

5. Aritmatika Sosial

Aritmatika sosisal adalah ilmu matematika yang membahas mengenai penghitungan dalam kegiatan sosial, seperti penghitungan jual-beli, penghitungan untung-rugi,  menghitung potongan harga (diskon), rabat, tara, bruto, atau neto.
Secara konsep, materi ini mirip dengan penghitungan ekonomi. Dengan menguasai materi ini, kamu dengan mudah menghitung laba yang kamu dapat setiap harinya, diskon yang tepat untuk barang daganganmu, dan pemberian bunga pinjaman.

6. Perbandingan & Aplikasinya

Perbandingan adalah sebuah materi matematika yang bertujuan untuk membuat nilai perbandingan dari beberapa hal. Dalam beberapa hal, perbandingan seringkali disebut dengan rasio (ratio). Pada umumnya, nilai perbandingan dipisahkan dengan tanda titik dua (:), seperti 4:5, 3:2, atau 3:1.
Pada umunya, ada 2 jenis perbandingan, yaitu: perbandingan senilai dan perbandingan berbalik nilai. Perbandingan senilai, yaitu sebuah perbandingan yang terjadi jika nilai dari suatu barang mengalami kenaikan/penurunan sama dengan nilai barang yang diperbandingkan. Perbandingan berbalik nilai, yaitu sebuah perbandingan yang terjadi jika nilai suatu barang mengalami kenaikan ketika barang yang lain mengalami penurunan, dan sebaliknya.
Pada kehidupan sehari-hari, perbandingan ini sering digunakan. Misalnya, perbandingan jenis senyawa kimia yang akan diujikan, perbandingan jarak wilayah, skala pada peta, perbandingan usia dalam statistika, atau perbandingan kecepatan.

7. Notasi Sigma

Notasi Sigma adalah sebuah metode yang digunakan untuk menuliskan penjumlahan dengan cara yang lebih singkat. Kamu bisa mengenali notasi sigma dari tanda yang digunakan, yaitu tanda sigma (∑).
Pada dasarnya, pencarian dan penggunaan notasi sigma di dunia sudah dimulai dari sejak jaman peradaban Yunani kuno. Beberapa ilmuwan Yunani ternama, seperti Archimedes, Phytagoras, ataupun Hippocrates, terlibat dalam pencarian ini. Beberapa tahun kemudian, beberapa peradaban, seperti cina, mesir dan arab, juga melakukan hal yang sama.
Untuk melakukan perhitungan matematika, notasi sigma amat memudahkan kamu, namun untuk melakukannya ada beberapa sifat notasi sigma yang harus kamu ketahui. Ketahui dengan lebih lengkap mengenai rumus aritmatika dasar mengenai notasi sigma dan kerjakan soal notasi sigma disini.

8. Barisan & Deret

Barisan & Deret adalah urutan bilangan dari sebelah kiri ke sebelah kanan dengan mengikuti sifat ataupun pola tertentu. Barisan & deret bilangan selalu mempunyai beberapa bilangan yang menjadi suku dalam sebuah barisan dan deret.
Materi ini membahas mengenai penghitungan barisan dan deret bilangan. Terlebih lagi, kamu akan bertemu dengan beberapa istilah, yaitu barisan aritmatika(suatu barisan dimana selisih dua angka yang berurutan nilainya tetap), deret aritmatika (jumlah bilangan yang terdapat dalam barisan), barisan geometri (suatu barisan dimana hasil bagi dua angka yang berurutan nilainya tetap), dan deret geometri (jumlah suku angka pada barisan geometri).

B. Logika

Pelajaran matematika juga mempelajari mengenai ilmu logika. Logika berfokus pada penggabungan dari kekuatan ilmu berpikir (logika) dan kemampuan pembuktian. Oleh karena itu, hasil yang didapat dalam materi logika harus sesuai dengan bukti yang valid.
Logika muncul sebagai salah satu cabang matematika pada pertengahan abad ke 19. Logika dimasukkan ke dalam matematika karena pada dasarnya, matematika merupakan kumpulan logika manusia yang disusun secara sistematis dan terorganisir sesuai dengan bidangnya.
Di dalam materi logika, kamu akan mempelajari mengenai beberapa hal, seperti: ilmu himpunan, logika matematika, modus ponens & tollens, dan induksi matematika. Logika juga menggali mengenai silogisme, yang merupakan temuan dari Aristoteles.

1. Himpunan

Materi pertama yang akan kamu pelajari adalah himpunan matematika. Himpunan adalah kumpulan benda-benda sebagai satu kesatuan, misalnya Jakarta adalah himpunan dari orang-orang dari berbagai suku dan ras atau rumah kamu adalah himpunan alat-alat rumah tangga.
Dalam mempelajari himpunan matematika, kamu akan membelajari banyak hal, seperti:

• Diagram Venn, sebuah diagram yang ditemukan oleh John Venn untuk menghitung himpunan yang berada pada sebuah bagian.
• Irisan himpunan, suatu himpunan yang memiliki anggota yang sama dengan himpunan lainnya. Irisan dilambangkan dengan tanda (∩).
• Gabungan himpunan, suatu himpunan baru yang terbentuk dari 2 anggota himpunan. Gabungan dilambangkan dengan tanda (∪)
• Komplemen himpunan, himpunan yang tidak terdapat pada satu himpunan inti.

2. Logika Matematika

Pengertian logika matematika yaitu cabang matematika yang menggabungkan aspek matematika dengan ilmu logika. Materi ini berfokus pada kekuatan pikiran manusia dan kekuatan pembuktian matematika.
Materi ini mulai dipelajari sejak akhir abad ke 19, bersamaan dengan pengembangan geometri, aritmatika, dan analisis matematika. Beberapa pelajaran yang akan kamu terima di bab ini antara lain: konjungsi, disjungsi, implikasi, dan penarikan kesimpulan (Modus Ponens & Tollens dan silogisme).

3. Induksi Matematika

induksi matematika merupakan suatu metode pembuktian langsung terhadap penyataan-pernyataan yang berhubungan dengan bilangan asli. Induksi matematika sudah dikembangkan sejak 370 SM ketika Plato di dalam buku Parmenides memberikan contoh pembuktian induktif. Tahun 1000 M, al-Karaji memberikan pembuktian implisit menggunakan induksi matematika.
Induksi matematika dilakukan dengtan 2 cara, yaitu kasus dasar dan langkah induktif.  Kasus dasar dilakukan untuk membuktikan pernyataan yang diberikan kepada bilangan asli pertama. Langkah induktif dilakukan untuk membuktikan bahwa pernyataan yang diberikan kepada setiap bilangan asli juga memberikan pernyataan kepada bilangan asli berikutnya.

C. Aljabar

Aljabar merupakan ilmu yang berhubungan dengan simbol (x, y) dan rumus matematika untuk mendapatkan hasil dari sebuah persamaan ataupun soal tertentu. Kata aljabar sendiri berasal dari bahasa arab al-jabr yang berarti penyatuan bagian yang rusak.
Ada 2 orang ilmuwan yang dianggap sebagai bapak aljabar, yaitu Diophantus, penemu persamaan Diophantine danMuhammad Al-Khwarizmi yang menerbitkan buku The Compendious Book on Calculation by Completion and Balancing.
Untuk mempelajari aljabar, kamu harus menguasai beberapa materi dalam aljabar, yaitu persamaan & pertidaksamaan, logaritma, eksponen, fungsi kuadrat, dan aljabar dasar.

1. Bentuk Aljabar

Untuk memahami materi ini, pertama-tama kamu perlu memahami soal bentuk-bentuk aljabar. Dalam materi ini, kamu akan dijelaskan mengenai sifat-sifat dasar aljabar, operasi dasar aljabar, dan pengertian beberapa istilah yang dipakai (variabel, koefisien, atau konstanta).
Ada 3 sifat-sifat dasar yang perlu kamu ketahui, yaitu komutatif (a+b=b+a), asosiatif ((a+b)+c=a+(b+c)), dan distributif (a(b+c)=ab+ac) atau (a(b-c)=(ab-ac)). Untuk operasi dasar, operasi aljabar mirip dengan operasi dasar aritmatika, seperti penjumlahan, pengurangan, perkalian, dan pembagian.Oleh karena itu, kamu sangat wajib memahami semua hal dasar.

2. Persamaan & Pertidaksamaan Satu Variabel

Persamaan & Pertidksamaan Satu Variabel adalah sebuah bentuk persamaan dan pertidaksamaan yang semua anggotanya memiliki satu variabel berpangkat satu. Kamu perlu memahami persamaan dan pertidaksamaan satu variabel ini sebelum menuju bentuk persamaan lainnya.
Perbedaannya adalah persamaan satu variabel menggunakan tanda hubung sama dengan (=), sedangkan pertidaksamaan satu variable menggunakan lambang-lambang pertidaksamaan, seperti lebih dari (>), kurang dari (<), lebih dari sama dengan (≥), kurang dari sama dengan (≤), dan tidak sama dengan (≠).

3. Bentuk Pangkat & Akar

Selanjutnya, bentuk pangkat & akar. Bentuk pangkat merupakan suatu bentuk penulisan perkalian bilangan dalam bentuk yang sederhana, sedangkan bentuk akar yaitu akar bilangan asli positif yang menghasilkan bilangan irrasional. Kamu akan sering melihat contoh bentuk pangkat (3² atau 7³) dan bentuk akar (√5 atau √37) di dalam teori dan rumus aljabar.
Di dalam materi bentuk pangkat, kamu akan mempelajari mengenai jenis-jenis bentuk pangkat (pangkat positif, pangkat negatif, pangkat nol, dan pangkat pecahan) dan operasi hitung bentuk pangkat (penjumlahan, pengurangan, perkalian, dan pembagian). Di sisi lain, materi bentuk akar akan menjelaskan mengenai operasi hitung bentuk akar (penjumlahan, pengurangan, perkalian), pemangkatan bentuk akar, dan bentuk akar istimewa.

4. Logaritma

Dalam matematika, logaritma adalah sebuah operasi yang merupakan kebalikan dari bentuk pangkat (eksponen). Bentuk pangkat mengajarkan kamu untuk menentukan nilai pemangkatan, sedangkan logaritma memberikan pemahaman untuk menentukan pangkat dari sebuah bilangan.
Logaritma pertama kali ditemukan dan dipakai pada abad ke 16. Melalui bukunya Mirifici Logarithmorum Canonis Descriptio (Description of the Wonderful Rule of Logarithms) tahun 1614, John Napier pertama kali mempublikasikan metode logaritma. Setelahnya, banyak ilmuwan, seperti Gottfried Leibniz dan Christian Huygens, turut mengembangkan logaritma.
Di masa kini, logaritma banyak digunakan untuk pemrograman komputer dan sains

5. Persamaan Kuadrat

Ketika masuk ke persamaan kuadrat, itu artinya bahwa kamu sudah mulai mendalami matematika dan aljabar. Persamaan kuadrat adalah bentuk persamaan dimana pangkat paling besar setiap variabelnya adalah 2. Dalam materi ini, kamu akan menemukan persamaan-persamaan seperti αx²+bx+c=0.
Dalam materi ini, kamu akan menjajal materi-materi yang semakin dalam, seperti pemfaktoran persamaan kuadrat, melengkapi kuadrat sempurna, rumus ABC, diskriminan persamaan kuadrat, jumlah & hasil kali akar, dan penyusunan persamaan kuadrat baru.

6. Pengertian & Jenis Fungsi

Fungsi adalah pemetaan semua anggota di daerah asal dengan semua anggota di daerah hasil. Dalam fungsi, setiap anggota di daerah asal harus dipasangkan dengan setiap anggota di daerah hasil. Oleh karena itu, jika ada anggota yang tidak dipetakan ataupun ada satu anggota di daerah asal yang mendapat 2 kali pemetaan, itu bukanlah fungsi.
Untuk mempelajari fungsi, kamu juga harus mengerti sifat-sifat dari fungsi, yaitu fungsi injektif (setiap anggota domain memiliki kawan berbeda di domain lain), fungsi surjektif (anggota b mempunyai pasangan di domain lain), dan fungsi bijektif (campuran antara ijektif dan surjektif). Kemudian, ada beberapa jenis fungsi yang harus kamu ketahui, antara lain: fungsi linear, fungsi kuadrat, fungsi harga mutlak, dan fungsi tangga.

7. Fungsi Kuadrat

Fungsi Kuadrat merupakan salah satu fungsi yang dipelajari dalam aljabar. Fungsi kuadrat adalah suatu fungsi dimana pangkat terbesar variabelnya adalah 2. Pada dasarnya, bentuk fungsi kuadrat mirip dengan persamaan kuadrat, namun bentuknya fungsi. Bentuk umum dari fungsi kuadrat adalah ƒ(x) = ax²+bx+c.
Di materi fungsi kuadrat, kamu akan mempelajari mengenai beberapa sub-bab, yaitu grafik fungsi kuadrat, titik balik fungsi kuadrat, dan aplikasi fungsi kuadrat. Selain itu, kamu juga akan bertemu dengan metode untuk menyusun fungsi kuadrat baru.

8. Pertidaksamaan Linear, Kuadrat, & Pecahan

Sebelum masuk ke materi ini, kamu perlu memahami konsep dari tiap materi di sub-bab ini. Pertidaksamaan linear adalah sebuah sistem dalam aljabar yang memiliki variabel berpangkat satu dan memiliki tanda pertidaksamaan diantaranya. Dalam materi ini, kamu juga akan dituntut untuk menggambarkan pertidaksamaan ke dalam bentuk grafik.
Selanjutnya, pertidaksamaan kuadrat merupakan sebuah sistem pertidaksamaan dimana setiap variabel yang ada maksimal hanya berpangkat dua. Untuk menyelesaikan sistem pertidaksamaan kuadrat, kamu bisa menggunakan interval garis bilangan ataupun grafik dari pertidaksamaan tersebut.
Pertidaksamaan pecahan yaitu sebuah sistem pertidaksamaan yang digambarkan dengan bentuk pecahan. Kamu bisa menggunakan garis bilangan untuk menyelesaikan pertidaksamaan pecahan.

9. Persamaan & Pertidaksamaan Bentuk Akar & Harga Mutlak

Secara garis besar, konsep persamaan dan pertidaksamaan bentuk akar yaitu sebuah sistem persamaan dan pertidaksamaan yang memasukkan sistem fungsi akar dalam matematika. Beberapa fungsi akar yang digunakan, yaitu fungsi linear, fungsi kuadrat, ataupun fungsi bentuk pecahan. Umumnya, kamu akan dituntut untuk mencari nilai x atau y di materi ini.
Selanjutnya, harga mutlak bisa dijabarkan sebagai jarak suatu bilangan terhadap titik 0 pada sebuah garis bilangan. Misalnya, x = 2 memiliki 2 harga mutlak yaitu x = 2 atau x = -2. Nah, konsep dasar harga mutlak ini bisa membantu kamu untuk menyelesaikan soal persamaan atau pertidaksamaan harga mutlak.

10. Sistem Persamaan

Dalam aljabar, ada 2 jenis sistem persamaan yang umumnya dipelajari, yaitu persamaan linear dan persamaan kuadrat. Sistem persamaan linear merupakan sistem persamaan yang variabelnya berpangkat satu, sedangkan persamaan kuadrat merupakan sistem persamaan yang variabelnya berpangkat 2.
Untuk menyelesaikan soal-soal sistem persamaan, ada beberapa metode penyelesaian yang bisa kamu gunakan, antara lain metode grafik (membuat grafik sehinggga ditemukan nilai x dan y), metode subtitusi (mengganti nilai satu variabel dalam persamaan), metode eliminasi (menghilangkan beberapa variabel dalam persamaan), dan metode eliminasi subtitusi (penggabungan metode eliminasi dan subtitusi).

11. Fungsi Komposisi & Fungsi Invers

Seperti yang sudah dijelaskan sebelumnya, fungsi adalah usaha untuk membuat pemetaaan dari himpunan A ke himpunan B. Jadi, fungsi komposisi yaitu sebuah sistem fungsi untuk membuat komposisi baru dari 2 himpunan yang ada, sedangkan fungsi invers adalah sistem fungsi untuk mencari relasi antar 2 himpunan yang dihitung.

12. Suku Banyak / Polinomial

Secara konsep, suku banyak adalah sebuah bentuk matematika yang terdiri dari variabel dan koefisien. Dalam suku banyak (polinomial), ada beberapa istilah yang harus kamu ketahui, yaitu suku dan konstanta dari polinom, peubah, koefisien polinom, konstanta, dan pangkat dalam polinom.
Materi mengenai suku banyak (polinomial) termasuk ke dalam matematika lanjutan yang akan kamu temukan pada jenjang pendidikan SMA. Beberapa sub-bab yang akan kamu hadapi antara lain, teorema sisa, teorema faktor, jumlah & hasil kali suku banyak, dan menyusun suku banyak baru.

13. Persamaan Eksponen & Logaritma

Kamu bisa mulai dengan mengenal konsep dari persamaan eksponen & logaritma. Persamaan eksponen adalah sebuah sistem persamaan dimana terdapat sebuah bilangan yang eksponennya memiliki sebuah variabel, sedangkan persamaan logaritma merupakan sistem persamaan yang mengadaptasi logaritma dan sifat dasar logaritma di dalam penyelesaiannya.
Dengan mempelajari persamaan eksponen & logaritma, itu berarti kamu sudah mulai menguasai materi-materi yang terdapat dalam aljabar. Untuk menyelesaikan persamaan eksponen & logaritma, hal pertama yang kamu lakukan adalah memahami sifat-sifat dasar dari persamaan eksponen dan logaritma.

14. Pertidaksamaan Eksponen & Logaritma

Selanjutnya, pertidaksamaan eksponen & logaritma. Pertidaksamaan eksponen adalah sebuah sistem yang terdapat dalam aljabar dimana eksponennya (pangkat) memiliki variabel dan terdapat tanda pertidaksamaan di dalamnya, sedangkan pertidaksamaan logaritma yaitu sistem yang memiliki logaritma di dalamnya.

D. Geometri Dimensi Dua

Geometri merupakan satu ilmu yang membahas mengenai unsur-unsur dan penghitungan bangun datar dan bangun ruang. Tentu, di materi ini kamu akan bertemu dengan rumus-rumus geometri untuk menghitung luas, keliling, ataupun volume bangun.
Geometri Dimensi Dua menjadi materi geometri dasar yang kamu harus pelajari. Dalam mempelajari geometri dimensi dua, kamu akan bertemu dengan aspek-aspek seperti: sudut, garis, dan bangun datar.
Belajar matematika mengenai geometri dimensi dua menjadi dasar bagi kamu untuk lanjut ke pembelajaran berikutnya. Materi ini akan kamu dapatkan secara bertahap dari jenjang SD, SMP, SMA, bahkan universitas.

E. Geometri Koordinat

Geometri Koordinat atau geometri analisis merupakan salah satu materi yang membahas geometri dengan mengaplikasikan teori-teori aljabar. Geometri koordinat juga sering dikatakan sebagai seni menentukan koordinat. Pada umumnya, geometri koordinat dilakukan dengan menggunakan sebuah sistem, bernama sistem kartesius.
Geometri koordinat pertama kali dicetuskan oleh seorang filsuf Perancis bernama Rene Descartes. Lewat bukunya La Geometrie , Rene Descartes memberikan sebuah hubungan antara geometri dan aljabar dalam penghitungannya.
Geometri koordinat ini perlu kamu pelajari karena berbagai jenis pekerjaan mengharuskan kemampuan pengenalan koordinat. Untuk itu, kamu perlu stay tune disini untuk menguasai semua materi tentang geometri koordinat.

F. Trigonometri

Trigonometri, membahas mengenai teori kesebangunan ruang. Kata trigonometri berasal dari 2 kata dalam bahasa Yunani,trigonon (tiga sudut) dan metro (mengukur).
Trigonometri sudah dipelajari sejak dari peradaban Mesir kuno, Babilonia, dan peradaban lembah Indus untuk kepentingan astronomi. Di matematika modern, trigonometri dipelajari untuk menghitung kesebangunan ruang, terutama segitiga.
Dalam belajar trigonometri, kamu juga akan mengenal istilah-istilah seperti: sinus, cosinus, tangen, secan, cosecan, dan cotangen.

G. Geometri Dimensi Tiga

Geometri Dimensi Tiga juga merupakan materi selanjutnya yang akan kamu pelajari. Materi ini akan kamu pelajari secara bertahap di jenjang Sekolah Dasar (SD), Sekolah Menengah Pertama (SMP) dan Sekolah Menengah Atas (SMA).
Di materi ini, kamu akan belajar mengenai pengukuran bangun datar, seperti balok, kubus, prisma, limas, tabung, kerucut, ataupun bola. Materi ini juga akan mengajarkan kamu mengenai materi titik tembus, irisan/penampang, geometri sudut, dan geometri jarak.
Seperti halnya geometri dimensi dua, kamu juga akan menemukan rumus matematika di geometri dimensi tiga. Rumus matematika yang diberikanpun tergantung dengan jenjang pendidikan.

H. Matriks

Matriks merupakan sebuah teknik penyusunan bilangan, simbol, ataupun unsur numerik lainnya menurut baris dan kolom. Unsur-unsur yang disusun di dalam sebuah matriks disebut juga dengan elemen atau anggota matriks.
Kata ‘matriks’ diambil dari sebuah kata dalam bahasa latin ‘matrix’ yang berarti rahim/kandungan. Istilah ‘matriks’ tidak digunakan sebelum tahun 1850. Tahun 1850, James Joseph Sylvester memperkenalkan istilah ‘matriks’, namun Arthur Cayleyyang dinobatkan sebagai bapak matriks dunia.

I. Vektor

Vektor adalah sebuah objek yang memiliki besaran dan arah, dan bisa dipanjangkan dengan vektor lainnya. Dengan kata lain, vektor adalah besaran jarak yang ditempuh dari suatu titik tertentu.
Kata ‘vektor’ diambil dari bahasa latin ‘vector’ yang berarti pembawa. Ilmu pengukuran vektor, pada awalnya, digunakan oleh para ahli astronomi di abad ke 18 untuk melihat pergerakan rotasi planet terhadap matahari.
Dalam pengukuran vektor, kamu juga bisa mengaplikasikan operasi-operasi aljabar seperti penambahan, pengurangan, cross product, dan dot product.

J. Transformasi Geometri

Transformasi Geometri adalah sebuah proses penentuan titik koordinat baru untuk menentukan posisi baru dari sebuah bangun pada sebuah bidang. Perubahan bangun ini bisa dilakukan dengan cara translasi (pergeseran), refleksi (pencerminan), rotasi (perputaran), dan dilatasi (pembesaran), stretching (regangan), dan shearing (gusuran).
Transformasi geometri dimulai ketika seorang ilmuwan bernama Felix Klein menjelaskan teorinya pada Erlangen Programtahun 1872. Ia mengemukakan bahwa geometri merupakan materi yang membahas mengenai kumpulan bangun yang memiliki sumbu simetri dan dengan sumbu simetri, bangun bisa ditransformasikan.
Sejak tahun 1872, transformasi geometri menjadi sebuah bagian yang tidak terpisahkan dalam ilmu hitung, terutama geometri.

K. Kalkulus

Kalkulus mempelajari mengenai perubahan unsur-unsur matematika. Kalkulus berfokus pada limit, turunan, integral, dan deret tak terhingga. Ada 2 cabang utama dari kalkulus yang perlu kamu ketahui, yaitu kalkulus differensial dan kalkulus integral.
Kalkulus pertama kali digunakan di abad ke 17. Materi ini dikembangkan oleh 2 ilmuwan kenamaan Isaac Newton danGottfried Leibniz. Isaac Newton lebih banyak mengaplikasikan kalkulus ke dalam ilmu fisika, sedangkan Gottfried Leibniz lebih kepada notasi-notasi kalkulus.
Kalkulus differensial adalah nilai turunan dari suatu fungsi, sedangkan kalkulus integral berfokus pada konsep penjumlahan yang berkesinambungan.

L. Peluang

Teori peluang adalah materi untuk mengetahui kemungkinan suatu kejadian akan terjadi. kemungkinan satu kartu, dadu, ataupun bola keluar bisa kamu perkirakan dengan teori peluang. Dengan materi peluang ini, kamu bisa memperkirakan kemungkinan kamu untuk memenangkan suatu permainan.
Girolami Cardano merupakan orang pertama yang mengembangkan teori peluang. Cardano mencari peluang seseorang untuk memenangkan perjudian dan menuliskan teorinya tersebut ke dalam buku Liber de Ludo Aleae (Book on Games of Changes) pada tahun 1565.

13. Statistika

Statistika adalah sebuah ilmu yang berfokus pada pengolahan data. Ada 2 macam data yang diolah dalam statistika, yaitu data tunggal dan data berkelompok. Data tunggal, yaitu data yang tidak memiliki interval diantara nilai yang akan dihitung, sedangkan data berkelompok adalah data dimana terdapat interval diantara nilai yang akan dihitung.
Dalam menjawab soal-soal matematika statistika, kamu akan menemui beberapa istilah yang harus kamu pahami, seperti Populasi (daerah yang akan dihitung), Sampel (besaran yang diambil dari sebuah populasi), Mean (nilai rata-rata), Modus (nilai yang paling sering muncul), dan Median (nilai tengah).
Statistika membantu kamu untuk menghitung beberapa besaran terkait dengan populasi yang akan kamu hitung, misalnya kamu ingin menghitung nilai rata-rata di kelasmu.